Practice Notes:
Teaching Math for All Learners
Welcome to our Blog
Check out our stories to learn more about the work of the All Learners Network. Our contributors include ALN Instructors, leaders, and math coaches. Click any of the photos below to read the full blog post.

Is integrity the new fidelity in the math classroom?
Published: April 19, 2024
Why Should Educators Use Math Menu?
Marilyn Burns was one of the first in the math education field to talk about using Math Menus. She identified three big questions that teachers consistently ask:

Proactive Design: Planning for All
My dad is a trim carpenter. He builds a variety of furniture, custom cabinetry, and trim, and has dabbled in barn door building. We moved into our new house about a year and a half ago and I knew I wanted a barn door as an option to close off my...

Exploring 4 Categories of Number Sense Routines
The first five to fifteen minutes of a math block set the tone for discourse and engagement during math class. At All Learners Network (ALN)), we refer to this time as Launch. This crucial time helps to position all students as mathematicians, as...
Playing with Numbers: Early & Joyful Math Interactions
We know that when young children have positive, early experiences engaging with math before kindergarten, it has a positive impact on their mathematical understanding later in school. “Early competence with number has proven to be a predictor of...

Seven Closure Activities for Your Math Block
Wrapping up a math lesson is an essential component of a balanced math block. All Learners Network (ALN) names this component Closure. Intentional closure in a math lesson is as beautiful as it is powerful. It is as much an opportunity for class...
What makes professional learning effective?
Educator professional development is a mixed bag in many school districts. Teachers are exposed to workshops and trainings on topics as diverse as dealing with blood-borne pathogens to content-specific work for individual disciplines. The quality of...

Disrupt Tracking in Math Classrooms
We are sorting, separating, and segregating students in the name of support services and differentiation in our education systems. Just consider all the ways students have been sorted into some version of “low, middle, and high” groups this school...

Free Math Intervention Resources for Educators & Specialists
Math intervention is a constant topic for many of us in preK-12 education. As an organization committed to supporting math pedagogy so all students can learn math, All Learners Network (ALN) frequently strategizes with districts and schools on how...

Countering Teaching Through Telling with 4 Inclusive Math Instruction Strategies
Picture this - a teacher stands at the front of the room. Their back is to you and they are writing an addition problem on the board: 24 + 37. They tell you to do what they are doing. “First, we line up the tens, then we line up the ones.” You copy...

Equipping Educators, Supporting Students: Partnering with ALN for a Summer Math Lab
All Learners Network (ALN)'s very own Sandi Stanhope and Christa Hagan-Howe talk through what the ALN Summer Math Lab is and how it works.

5 Free Workshop Recordings to Further Inclusive Math Instruction
Accessible and engaging professional development for math educators is always on our minds here atAll Learners Network (ALN). We are committed to supporting teachers and pedagogy so all students can access quality math instruction. We do this...

The Five Key Components for Unlocking Math Progress
All Learners Network (ALN) is committed to improving math pedagogy so that all students can access quality math instruction. We know that it is time to move away from antiquated notions around math education and focus on strong pedagogy. It is...
A Call to Stop Labeling Our Students
Recently, the All Learners Network (ALN) leadership team worked on a five-year plan. We dreamed big with the goal of spreading our mission around the country. In this projection, we designed a plan aimed at supporting thousands of districts,...

Why does high school math need a makeover?
There is no shortage of international studies to cast doubt on the effectiveness of American math instruction. Trends in International Mathematics and Science Study (TIMSS) and Programme for International Student Assessment (PISA) are two studies...

Building Confidence and Increasing Inclusion Through Launch
What is inclusion in a classroom really? Inclusion is talked about in education in many different ways and takes on many different forms. Inclusion is more than just being in the room. It is more than ‘just’.

Why Should ALL Math Blocks Include Launch?
At All Learners Network (ALN), we start every balanced math block with Launch. Launch is typically about 5-15 minutes, depending on your time and schedule, and focuses on building number sense, reasoning, community and productive math discourse....

Making Math Lessons More Inclusive: ALN Problem Introduction Protocol
What if there was a way to get students more comfortable sharing ideas during a math lesson? What if there was a way to reduce the amount of “I don’t knows” during a math lesson?

Math as a Door Opener
All means all. Not “some” or “most,” but every single person deserves to have a humanizing learning math experience that affirms themselves as the capable, competent math thinkers that they are. As educators, we must consider all aspects of a person...

New Free Membership Level to All Learners Online (ALO)
All Learners Online (ALO) is the self-paced professional learning and math instructional resources platform by All Learners Network (ALN). ALO delivers its members with high quality self-paced professional learning, math resources, and more. ALO...


Unpacking Belonging in Math Class
Why is belonging in math class so important?
Feeling a sense of belonging is a vehicle to engagement. Engagement promotes both learning and empowerment as an expert learner. At All Learners Network (ALN), we believe in opening the doors to all...

Why do the High Leverage Concepts (HLCs) focus on one skill?
This blog post pulls from chapter three of our book, Teaching Math for All Learners: Teaching educators to use effective strategies to help all children learn math.
What is math coaching? What is not math coaching?
All Learners Network (ALN) facilitators Erin Oliver and Tara Trudo pull from their experiences as classroom teachers, interventionists, math specialists, and coaches to collaborate on this basic coaching primer.

Strengthen Resilience with Math Anxiety
You hear the chime. Chairs scrape across the floor. You see your classmates walk towards the meeting space and find a spot on the rug. Your teacher gets out the easel markers and some linking cubes. It is time to start math. What is happening in...

What does an intervention cycle look like?
All educators can frame the process of their work with students as a cycle. All Learners Network (ALN) particularly recommends this specific framing to special educators and interventionists, or any teacher working with students in small groups.
...

What Do I Do With a Small Group?
Whether you are a classroom teacher, an interventionist, special educator, English as a second language teacher or other educator you might be wondering what do I do for small group math instruction?
We know all kids do not learn math at the same...

Why Concrete Tools Matter in ALL Math Classrooms
Concrete tools (manipulatives) support access, equity, universal design and differentiation in every math classroom. Manipulatives support mathematical connections and deep understanding. So why are they missing in so many math classrooms,...

How to Plan for Sustainable, Lasting Math Improvement in Schools & Districts
Math pedagogy is the key to improving math performance and math understanding for all students. Pedagogy is the single most important element in instruction to improve math performance and understanding.Teachers are the critical element in improving...

The Background on the Newly Revised HLC Learning Progressions
All Learners Network (ALN) originally created the High Leverage Concepts (HLC) Learning Progressions as a resource for classroom teachers, math interventionists, and special educators who create learning opportunities for their students daily. We...
How do we encourage playful, productive struggle in Math Menu?
Our goal in Math Menu is for students to feel both relaxed and curious. Let’s use a recess analogy to help visualize our menu practice. At recess, students are independent and engaged in an activity of their choosing. They are motivated, playful and...

What is a Professional Learning Outreach Coordinator?
Here at ALN, our mission is paramount in everything that we do. We’re constantly visiting our decision-making process and asking, “does this decision work with our mission in the way that we would want?”

All Learners Network's Evidence-Based Practices Alignment
Evidence-based practices (EBPs) are specific strategies, activities, or programs that have been found to be effective for improving student outcomes and backed by rigorous, high-standard research, replicated with positive outcomes (What Works...

What is Explicit Systematic Instruction?
How can you support your students in interventions so that they are building conceptual understanding and connecting mathematical concepts and strategies to strengthen their understanding? One recommendation in the IES practice guide from What Works...

Discourse in the Mathematics Classroom
What is discourse and why does it matter?
Discourse is the communication of ideas where there is interaction between students' own thoughts and ideas and the consideration and examination of the ideas of others’ to make meaning and grow collective...

What is Specialized Math Instruction?
Specialized Math Instruction (SMI) focuses on improving instructional techniques–or pedagogy– of all educators for teaching mathematics for all students.

A Case for High Quality Math Instruction for Students with Complex Needs
I would like to discuss a topic dear to me - the importance of high quality instruction for math students with complex cognitive needs. In the state of Vermont, these students tend to fall under the disability category of Intellectual Disability. My...

Purposeful Change: The ALN Rapid Cycle of Inquiry
A group of math coaches and I gathered for a local PLC meeting. We had been looking at student work and discussing some of the problems of practice facing the teachers in our buildings. In any gathering of educators, it’s pretty easy to articulate...

Establishing Classroom Culture
Establishing a classroom culture within the first six weeks of school is crucial for the success of a learning community. To facilitate an inclusive community culture, educators should establish routines and expectations with students, use language...

Inclusion and MTSS
I spend a lot of time in schools in many different grade levels and while there are more differences than similarities in the goings on of a 1st grade classroom and a 10th grade one, a major similarity is the question of inclusion. How does one...

Establishing a Feedback Culture
Use Student Work as Feedback We are in the business of being responsive.As educators we strive to establish a thriving feedback culture in our classrooms enriched by constantly looking at formative assessment data and responding. When armed with...

Math Coaches Make an Impact
Coaches provide support for teachers who have multiple demands through job embedded professional development. One key element essential to effective math instruction, that a math coach in particular provides, is supporting teacher knowledge of...

Problem Introduction Protocol (Updated)
About five years ago, several educators and ALN facilitators developed a Problem Introduction Protocol. We wanted to create a way in which we could introduce problems during the Main Lesson that would provide math access to all students. We’ve had a...

David’s Math Class: A Story of Inclusion
Often, when we talk about differentiation and inclusion, the responsibility is put upon the teacher to create, provide, and derive the means for low floor/high ceiling tasks (with multiple entry points) so all students may access the learning...

Differentiation - What Is It?
What is differentiation and where can it be applied?A differentiated classroom is facilitated by an educator's timely and ongoing response to student needs. Educators target and implement strategies and tools that provide access and inclusion and...

MTSS and the ALN Lesson Structure
Schools and classrooms are filled with diverse learners who all have their own individual knowledge and needs when it comes to learning. A Multi-Tiered or Multi-Layered System of Support (MTSS) provides a system in which educators can meet the needs...

Perseverance and Growth Mindset
No matter how many years of experience we’ve logged as educators, we all have to put in the work at the beginning of a new school year to build our classroom culture. This always starts with student relationships.
What do special educators need?
What do new Special Education teachers need most? More support for teaching math!

Systems Matter
I began my career in education because I believed it was a broken system that we could mend. My senior year I read Jonathon Kozol’s The Shame of the Nation and became convinced that the way to solve poverty in our country was to...

Why Math Menu Matters Even More Right Now
This school year has so many of us feeling like our first year teacher-selves, struggling with the work and effort that is required when you’re learning how to do something new.
It feels like we are facing more obstacles than...

Precision of Language
“Wow this game is really hard!” my aunt told my son while playing an arcade game. It’s easy to drop the token in and watch it land on the wheel, it’s just not likely that it lands exactly in the winning spots. I thought about her choice of words...

Ask a Smaller Question
I just finished working with a large group of teachers in Montpelier. They were inquisitive and eager. In the exit slips, several participants asked for more information about using questions to teach. This post is a response to...

30 Minute Intervention Block Using Math Menu
At Malletts Bay School, we had a set 30 minute intervention block beyond what we call “First Instruction.” My everyday math block consisted of about 55 minutes for the math lesson that day and then an additional 30 minutes set aside for...

Using Work Places in Bridges to Differentiate and Support All Learners
The blog is back from the holidays with a piece from Essex Westford School District on a topic that has come up numerous times in ALN meetings and workshops. How can I use Bridges for Differentiation? Here is how one district responded to this...
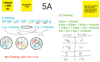
Jamboard Routine for 3 Act Math Tasks
After April vacation, I polled my fifth and sixth grade math lab groups to see how they wanted to close out the year together. I told them that in our last intervention cycle of the year we had two options.
I could design team problem-solving...

Commitment to Equity: Current Climate Demands a Need to Post Again
We are once again bearing witness to violence and racism in our country targeted at people within the Asian community. We are uniting with those who are facing incidents of hate. We once again want to reiterate our commitment to equity.
We stand...

Pick the Mini-Marshmallows
On a cold afternoon after my boys had been out sledding we were making hot chocolate with marshmallow of course! My youngest commented on how tiny the marshmallows were in comparison to the jumbo ones we use for roasting over the fire. The...
Math Learning in the time of COVID
As we enter 2022 we hope the new year brings health and reduced stress in schools, for staff and students alike. As we embark on year 3 of a pandemic, we continue to face challenges - staffing issues, absences due to sickness and quarantine, and...
From “Hey guys!” to “Hey y’all!”
I’m working on breaking a deeply ingrained habit of addressing groups of people as “guys”. I’ve played on sports teams my entire life and “guys” is just part of the sports lingo. I’ve used the word so often that now I use it...

ALN Commitment to Equity
In the wake of the murder of George Floyd, we wish to state unequivocally: Black lives matter.
We stand with those protesting the brutalization of people of color by police.
We stand with those fighting against the white supremacy culture that...

Conscious Discipline and Math Learning
This week we hear from Paige Benedict about Conscious Discipline – an approach to managing challenging behaviors with integrity and respect. Since we hear quite a bit about the prevalence of these behaviors, we thought this was an important...

Best Practices Support ALL Learners
When you think about your students and consider instruction you might have a particular child in mind. Maybe you are considering a multilingual learner, or a student who is on an IEP, maybe a student who is differently abled, or one that has not...

Finding Math Outside
Teaching during a global pandemic has brought about many changes and some of those have been good things that have moved teaching, learning and student engagement forward in a positive way. One change I hope sticks around is getting kids outside...

Math Trips at Folino’s
This idea emerged after a year of working on the All Learner’s Project and a summer spent working at the Folino’s pizza restaurant in Burlington.
One of the reasons I joined the All Learner’s Network is the High Leverage Concepts....

